Quantum fluctuations and driving fields affect or outright change the excited state properties of matter in and out of equilibrium. They open possibilities to realize new (transient) quantum phenomena due to the modulation of electronic excitation (quasiparticle-quasiparticle) couplings.
Our group works on the boundary of condensed matter theoretical chemistry, physics, and materials science. We develop approaches to understand dynamical quasiparticle correlations in materials, low-dimensional semiconductors, molecules, and quantum interfaces.
Dynamical quantum interactions in realistic systems were often deemed untractable by conventional theoretical techniques. We combine quantum many-body methods with new algorithms to break the current computational limitations and apply advanced theory to realistic nanoscale systems.
Our research is funded by NSF (DMR), DOE (BES/ASCR), and BSF. We rely on our own first principle codes. Our research requires the use of high-performance computing resources kindly provided by UCSB, NSF (XSEDE), and DOE (NERSC).
Many-body interactions in materials
We investigate a wide range of systems in which long-range dynamical correlations (due to fluctuations or the presence of driving fields) substantially change the excited states (=quasiparticles): low dimensional materials, complex molecular assemblies, interfaces, and defect states.
Besides the quasiparticle states formed in equilibrium conditions, our group is also developing new theoretical and computational techniques to decsribe the dynamics of non-equilibrium quantum many-body states. Here, the properties of materials can be changed drastically and the systems can be driven to novel behaviors. Targeted realization fo quantum states represent an untaped opportunity to modulate and control peroperties of matter at the level of individual electrons and their couplings to collective excitations (e.g., lattice vibrations or transient magnetic orderings). For details, you can see our invited perspective paper here.
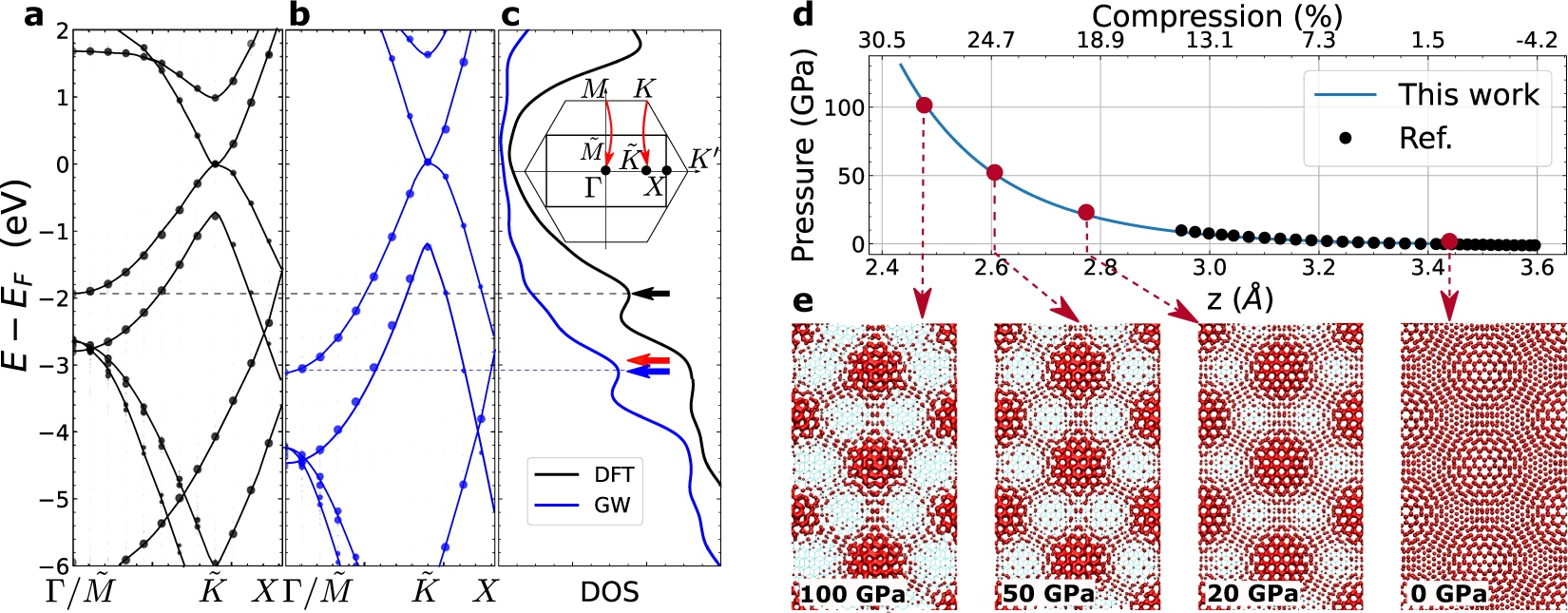
We study many-body interactions in systems that hold promise for quantum information storage and manipulation. For instance, we developed and applied new methods to investigate quasiparticle interactions and localization in twisted 2D semiconductors/semimetals. The emerging localized electronic states are associated with strong correlation and superconductivity; their behavior is strongly affected by non-local fluctuations of the weakly correlated electrons surrounding them.
Similarly, we inspect quantum interfaces hosting quantum defect states whose optical excitations are strongly coupled to the environment: quantum defects or even molecules in highly disordered polarizable media (selected as the Journal of Physical chemistry editor's choice for 2021).
Method Development
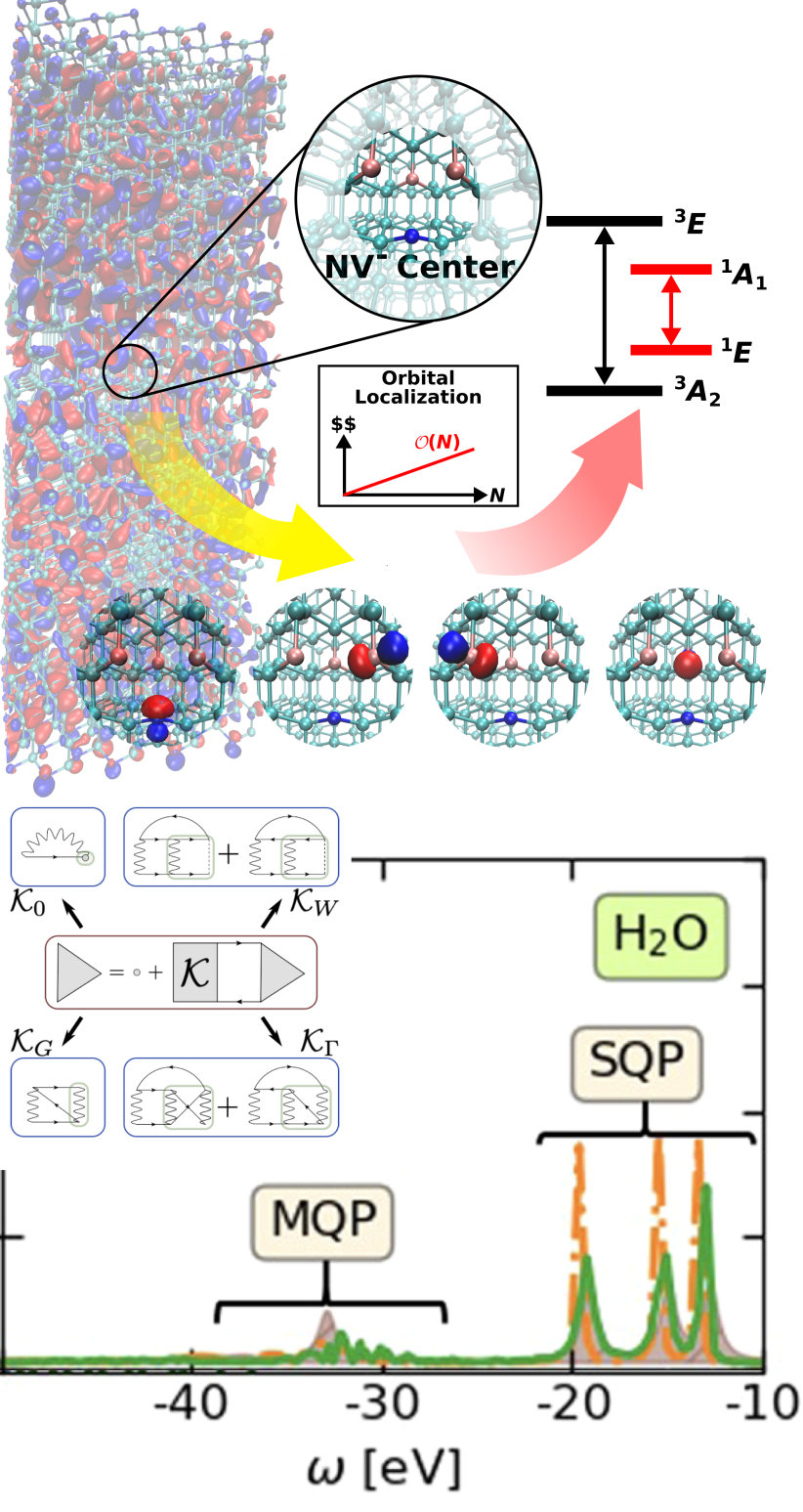
We specialize in the development of techniques to compute the dynamics of electron-electron interactions. We rely on many-body diagrammatic methods and downfolding that describe the excitations in terms of the quasiparticle dynamics. The methods are in quantitative agreement with experiments and directly provide access to observables (i.e., they can be directly linked to experiments). We have recently developed the Real-Time Dyson Expansion scheme, a many body method for first principles prediction of time resolved spectra including emergent quasiparticle states.
Typical implementations are time-consuming and can be applied only to small systems. We instead employ efficient real-time Monte-Carlo sampling of quasiparticle states and decomposition of quantum mechanical operators. The resulting computational techniques scale linearly with the system size, and we readily treat systems with thousands of atoms.
We have introduced a new method to compute non-local vertex corrections (GWGamma) - a step beyond the widely applied GW approximation. This approach significantly expands the applicability of the many-body perturbation theory and improves the agreement between theoretical predictions and experiments. Further, we demonstrated that it captures interactions of multiple quasiparticles and strong couplings to collective excitations.
Our group leads a SciDAC ("Scientific Discovery through Advanced Computing") center focusing on real-time dynamics of driven correlated electrons in quantum materials that explores new theoretical approaches for ultrafast and driven non-equilibrium phenomena in quantum materials.
Pictures from: Weng, Romanova, Apelian, Song, Vlcek (2022) J Chem Theory Comput: https://pubs.acs.org/doi/full/10.1021/acs.jctc.2c00315
Mejuto-Zaera, Vlcek (2022) Phys Rev B: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.106.165129
Mejuto-Zaera, Weng, Romanova, Cotton, Whaley, Tubman, Vlcek (2021) J Chem Phys https://aip.scitation.org/doi/full/10.1063/5.0044060
